Iterative Projection and Matching: Finding Structure-preserving Representatives and Its Application to Computer Vision

 

Publication:

Code: You can find the code for IPM here.

Presentation: You can see our IPM presentation here.

Introduction

The goal of data selection is to capture the most structural information from a set of data. This paper presents a fast and accurate data selection method, in which the selected samples are optimized to span the subspace of all data. We propose a new selection algorithm, referred to as iterative projection and matching (IPM), with linear complexity w.r.t. the number of data, and without any parameter to be tuned. The computational efficiency and the selection accuracy of our proposed algorithm outperform those of the conventional methods. Furthermore, the superiority of the proposed algorithm is shown on active learning for video action recognition dataset on UCF-101; learning using representatives on ImageNet; training a generative adversarial network (GAN) to generate multi-view images from a single-view input on CMU Multi-PIE dataset; and video summarization on UTE Egocentric dataset. In summary, this paper makes the following contributions:

• The complexity of IPM is linear w.r.t. the number of original data. Hence, IPM is tractable for larger datasets.
• IPM has no parameters for fine tuning, unlike some existing methods. This makes IPM dataset- and problem-independent.
• Robustness of the proposed solution is investigated theoretically.
• The superiority of the proposed algorithm is shown in different computer vision applications.

 

Method

We propose a novel representative-based selection method, referred to as Iterative Projection and Matching (IPM). Time complexity order of computing the first singular component of an M × N matrix is O(MN). As the proposed algorithm only needs the first singular component for each selection, its time complexity is O(KNM), which is much faster than convex  relaxation-based algorithms. Moreover, IPM performs faster than K-medoids algorithm.

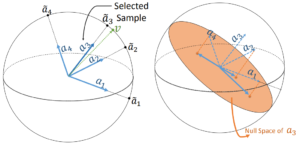
The above figure shows an intuitive example for one iteration of the proposed algorithm. First, the leading singular vector is computed, and then the most correlated sample in the dataset is matched with the computed singular vector. Next, all data are projected onto the null space of the matched sample. The projected data are ready to perform one more iteration, if needed. These iterations are terminated either by reaching the desired number of selected samples or a given threshold of residual energy. Data selection algorithms are vulnerable to outlier samples.

Since outlier samples are more spread in the space of data, their span covers a wider subspace. However, the spanned subspace by outliers may not be a proper representative subspace. Our proposed algorithm computes the first singular vector as the leading direction in each iteration. We show here that this direction is the most robust spectral component against changes in the data.

Application: Active Learning

Active learning aims at addressing the costly data labeling problem by iteratively training a model using a small number of labeled data, and then querying the labels of some selected data, using an acquisition function.  Now, the fundamental question in active learning is: Given a fixed labeling budget, what are the best unlabeled data instances to be selected for labeling for the best performance?

In many active learning frameworks, new data points are selected based on the model uncertainty. However, the effect of such selection only kicks in after the size of the training set is large enough, so we can have a reliable uncertainty measure. In this section, we show that the proposed selection method can effectively find the best representatives of the data and outperforms several recent uncertainty-based and algebraic selection methods.

The selection is performed on the convolutional features extracted from the last convolutional layer of the network. The table shows the accuracy of the trained network at each active learning cycle for different selection methods.

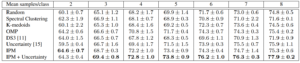
It is evident that, during the first few cycles, since the classifier is not able to generate reliable uncertainty score, uncertainty-based selection does not lead to a performance gain. In fact, random selection outperforms uncertainty-based selection. On the other hand,  IPM is able to select critical samples. In the first few active learning cycles, IPM is constantly outperforming other methods, which translates into significant reductions in labeling cost for applications such as video action recognition.

As the classifier is trained with more data, it is able to provide us with better uncertainty scores. Thus to enjoy the benefits of both IPM and uncertainty-based selection, we can use a compound selection criterion. For the extremely small datasets, samples should be selected only using IPM. However, as we collect more data, the uncertainty score should be integrated into the decision making process. Our proposed selection algorithm, unlike other methods, easily lends itself to such modification. This compound selection criterion leads to better results for larger dataset sizes.

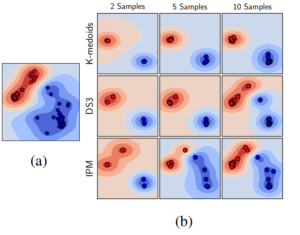
The above figure shows the t-SNE visualization of the selection process for two randomly selected classes of UCF-101.  To visualize the structure of the data, the contours represent the decision function of an SVM trained in this 2D space. This experiment illustrates that each IPM sample contains new structural information, as the selected samples are far away from each other in the t-SNE space, compared to other methods. Moreover, it is evident that as we collect more samples, the structure of the data is better captured by the samples selected by IPM, compared to other methods selecting the same number of representatives. The decision boundaries of the classifier trained on 5 IPM-selected samples look very similar to the boundaries learned from all the data.

For a more qualitative investigation, the above  figure shows frames from the first selected representative by IPM (top row) and DS3 (bottom row) for a few classes of UCF-101 dataset. In general, in the clip selected by IPM, the critical features of the action, such as barbell, violin, and kayak, are more visible and/or the bounding box for the action is bigger.

 

Still under construction. For inquiries, please contact zaeemzadeh -at- knights.ucf.edu