Project page for

Select to Better Learn: Fast and Accurate Deep Learning using Data Selection from Nonlinear Manifolds,

Joneidi, Mohsen ; Vahidian, Saeed ; Esmaeili, Ashkan ; Wang, Wijia ; Rahnavard, Nazanin ; Lin, Bill ; Shah, Mubarak

In proceedings IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2020 .

Codes: You can find the code for Spectrum Pursuit (SP) and Kernel SP here.

Presentation: You can see the presentation here.

Paper: You can download the paper here.

Introduction:

Finding a small subset of data whose linear combination spans other data points, also called column subset selection problem (CSSP), is an important open problem in computer science with many applications in computer vision and deep learning. There are some studies that solve CSSP in a polynomial time complexity w.r.t. the size of the original dataset. A simple and efficient selection algorithm with a linear complexity order, referred to as spectrum pursuit (SP), is proposed that pursuits spectral components of the dataset using available sample points. The proposed non-greedy algorithm aims to iteratively find K data samples whose span is close to that of the first K spectral components of entire data. SP has no parameter to be fine-tuned and this desirable property makes it problem-independent. The simplicity of SP enables us to extend the underlying linear model to more complex models such as nonlinear manifolds and graph-based models. The nonlinear extension of SP is introduced as kernel-SP (KSP). The superiority of the proposed algorithms is demonstrated in a wide range of applications.

 

Method:

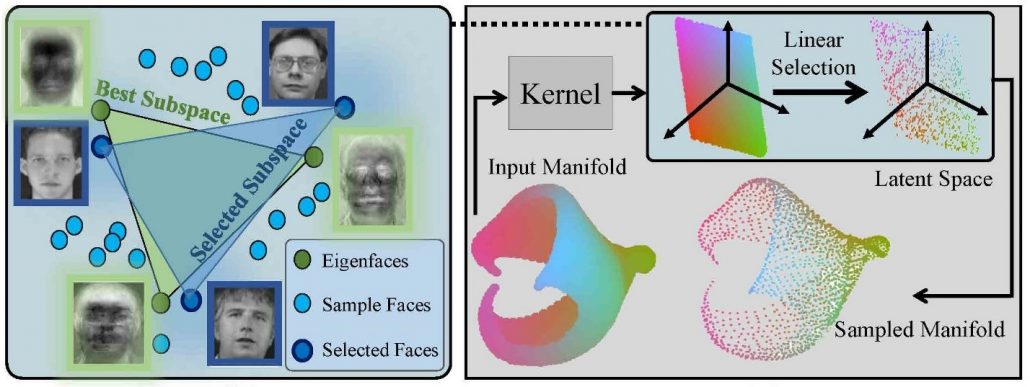
An efficient non-greedy algorithm is proposed to solve CSSP with a linear order of complexity. The proposed subspace-based algorithm outperforms the state-of-the-art algorithms in terms of accuracy for CSSP. In addition, the simplicity and accuracy of the proposed algorithm enable us to extend it for efficient sampling from nonlinear manifolds. The intuition behind our work is depicted in the following figure. Assume for solving CSSP, we are not restricted to selecting representatives from data samples, and we are allowed to generate pseudo-data and select them as representatives. In this scenario, the best K representatives are the first K spectral components of data according to definition of singular value decomposition.

However, the spectral components are not among the data samples. Our proposed algorithm aims to find K data samples such that their span is close to that of the first K spectrum of data. We refer to our proposed algorithm as spectrum pursuit (SP). This figure shows the intuition behind SP and also it shows a straightforward extension of SP for sampling from nonlinear manifolds. We refer to this algorithm as Kernel Spectrum Pursuit (KSP).

Our main contributions can be summarized as:

• We introduce SP, a non-greedy selection algorithm with linear order complexity w.r.t. the number of original data points. SP captures spectral characteristics of dataset using only a small number of samples. To the best of our knowledge, SP is the most accurate solver for CSSP.
• Further, we extend SP to Kernel-SP for manifold-based data selection.
• We provide extensive evaluations to validate our proposed selection schemes. In particular, we evaluate the proposed algorithms on training generative adversarial networks, graph-based label propagation, few shot classification, and open-set identification. We demonstrate that our proposed algorithms outperform the state-of-the-art algorithms.

Applications:

 

 

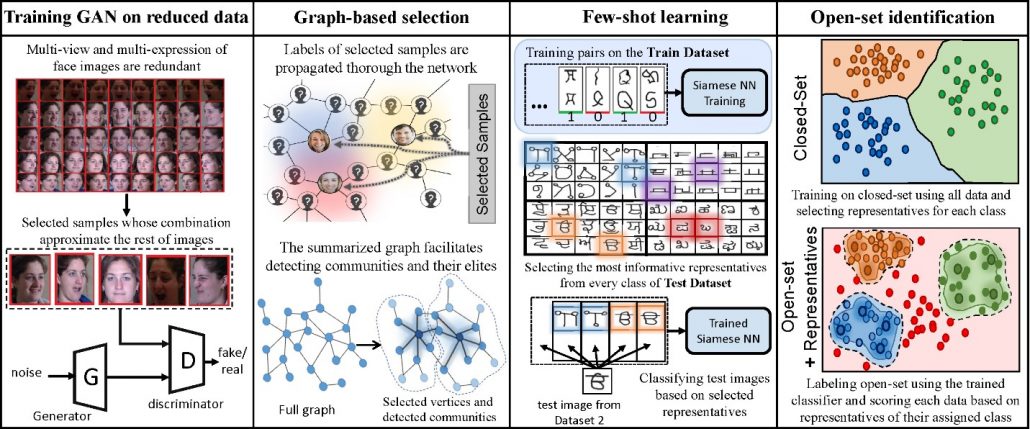
Training GAN: None of existing frameworks from training a GAN benefit from smart samples selection to expedite the training process. Here, we present our experimental results on CMU Multi-PIE Face Database for representative selection. We use 249 subjects with various poses, illuminations, and expressions. We use the selected samples to train a generative adversarial network (GAN) to generate multi-view images from a single-view input.

 

Graph-based Semi-supervised Learning:  we consider the graph convolutional neural network (GCN) that serves as a semi-supervised classifier on graph-based datasets. Indeed, a GCN takes a feature matrix and an adjacency matrix as inputs, and for every vertex of the graph produces a vector, whose elements correspond to the score of belonging to different classes. The neural network is trained based on semi-supervised learning, i.e., the network is fed with the feature and adjacency matrices of the entire graph while the loss is only computed on the labeled vertices. Here the labeled vertices correspond to the subset of vertices that is selected by applying our proposed algorithm.

 

Graph Summarization: Clusters (also known as communities) in a graph are those groups of vertices that share common properties. Identification of communities is a crucial task in graph-based systems. We design an experiment to find the vertices with a central position on several types of graphs.

 

Few Shot Learning: We adopt the Omniglot dataset and split it into three subsets for training, validation, and test, each of which consists of totally different classes. A Siamese network trained on training pairs to distinguish inter-class and intra-class pairs. After being fully trained on the sampled pairs, the model is developed for few-shot classification. In other words, if the model is accurate enough to distinguish the identity of classes to which the pairs belong to, given few representatives of a specific class, a trained Siamese network could serve as a binary classifier that verifies if the test instance belongs to this class.

 

Open-Set Identification: The open-set identification problem is addressed employing propose selection method, which results in significant accuracy improvement compared to the state-of-the-art. In open-set identification, test data of a classification problem may come from unknown classes other than the  classes employed during training, and the goal is to identify such samples belong to open-set and not the known labeled classes. Employing the entire closed-set data during the training procedure leads to inclusion of untrustworthy samples of the closed-set.