Norm-Preservation: Why Residual Networks Can Become Extremely Deep?
Paper:
- Alireza Zaeemzadeh, Nazanin Rahnavard, and Mubarak Shah, “Norm-Preservation: Why Residual Networks Can Become Extremely Deep?,” IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), in press 2020.
Code:
Augmenting neural networks with skip connections, as introduced in the so-called ResNet architecture, surprised the community by enabling the training of networks of more than 1,000 layers with significant performance gains. This paper deciphers ResNet by analyzing the effect of skip connections, and puts forward new theoretical results on the advantages of identity skip connections in neural networks. We prove that the skip connections in the residual blocks facilitate preserving the norm of the gradient, and lead to stable back-propagation, which is desirable from optimization perspective. We also show that, perhaps surprisingly, as more residual blocks are stacked, the norm-preservation of the network is enhanced. Our theoretical arguments are supported by extensive empirical evidence.
Can we push for extra norm-preservation? We answer this question by proposing an efficient method to regularize the singular values of the convolution operator and making the ResNet’s transition layers extra norm-preserving. Our numerical investigations demonstrate that the learning dynamics and the classification performance of ResNet can be improved by making it even more norm preserving. Our results and the introduced modification for ResNet, referred to as Procrustes ResNets, can be used as a guide for training deeper networks and can also inspire new deeper architectures.
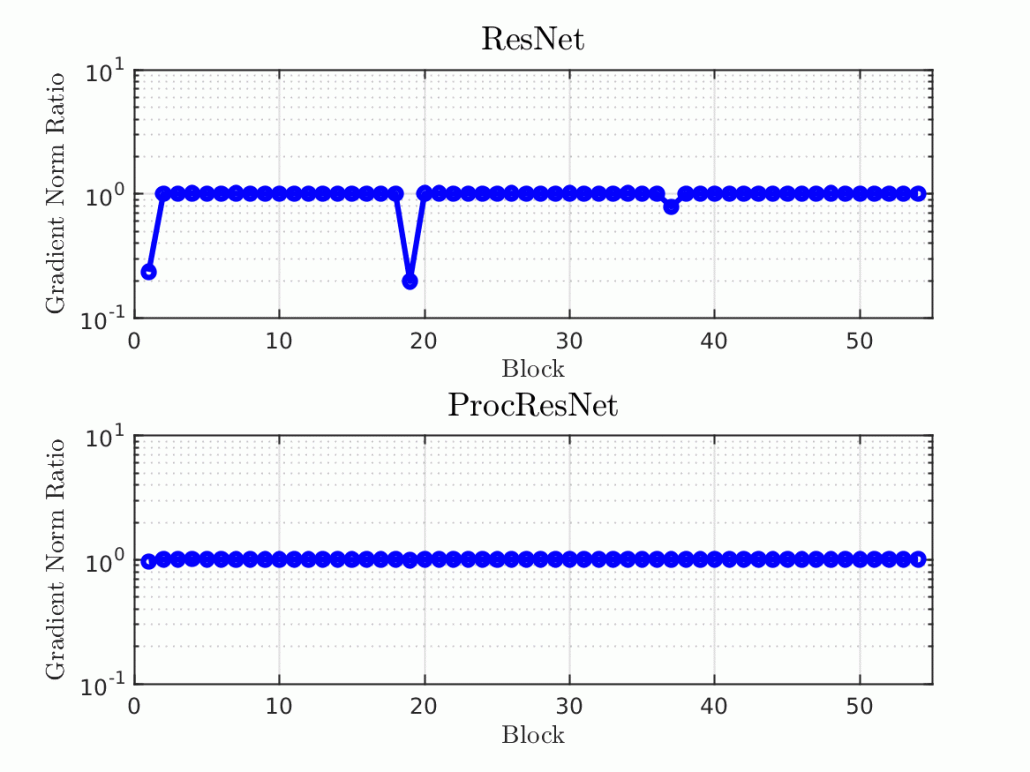
This following figure both validates our theoretical arguments and clarifies some of the inner workings of ResNet architecture, and also shows the effectiveness of the proposed modifications in ProcResNet. It is evident that addition of identity skip connection makes the blocks increasingly extra norm-preserving Furthermore, we have been able to enhance norm-preserving property by applying the proposed changes on the transition blocks. Our experiments validate our theoretical investigation by showing that (i) identity skip connection results in norm preservation, (ii) residual blocks become extra norm-preserving as the
network becomes deeper, and (iii) the training can become more stable through enhancing the norm preservation of the network. Our proposed modification of ResNet, Procrustes ResNet, enforces norm-preservation on the transition blocks of the network and is able to achieve better optimization stability and performance. For that we propose an efficient regularization technique to set the nonzero singular values of the convolution operator, without performing singular value decomposition.